Jeu web d'introduction à la cryptographie
J'ai perdu
Contexte cryptographique
La faiblesse principale des méthode de cryptographie symétrique, c'est-à-dire où la même clé sert à coder et décoder le message, est le problème de l'échange de clé. En effet, pour qu'Alice puisse décoder le message que Bob lui a envoyé, Bob doit aussi trouver le moyen d'envoyer la clé à Alice. Si les deux sont perpétuellement écouté par un espion Eve, alors il est certain que le message va pouvoir être décodé par Eve.L'un des moyens les plus connus pour résoudre le problème de l'échange de clé est le fameux téléphone rouge qui permettait aux Etats-Unis et à l'URSS de communiquer secrètement. Ce dispositif, qui n'est ni un téléphone ni rouge, a évolué au fil des progrès en cryptographie. La méthode utilisée était le chiffre de Vernam, parfaitement sûr à condition bien sûr que la clé ne soit pas interceptée. Pour ce faire, les clés circulaient dans des valises diplomatiques. Ainsi, le téléphone rouge permettait une communication parfaitement sûre entre deux personnes dans le monde, une limite de la cryptographie symétrique.
L'objectif de la cryptographie asymétrique est de permettre une communication sécurisée entre les particuliers, une révolution pour la vie privée des individus.
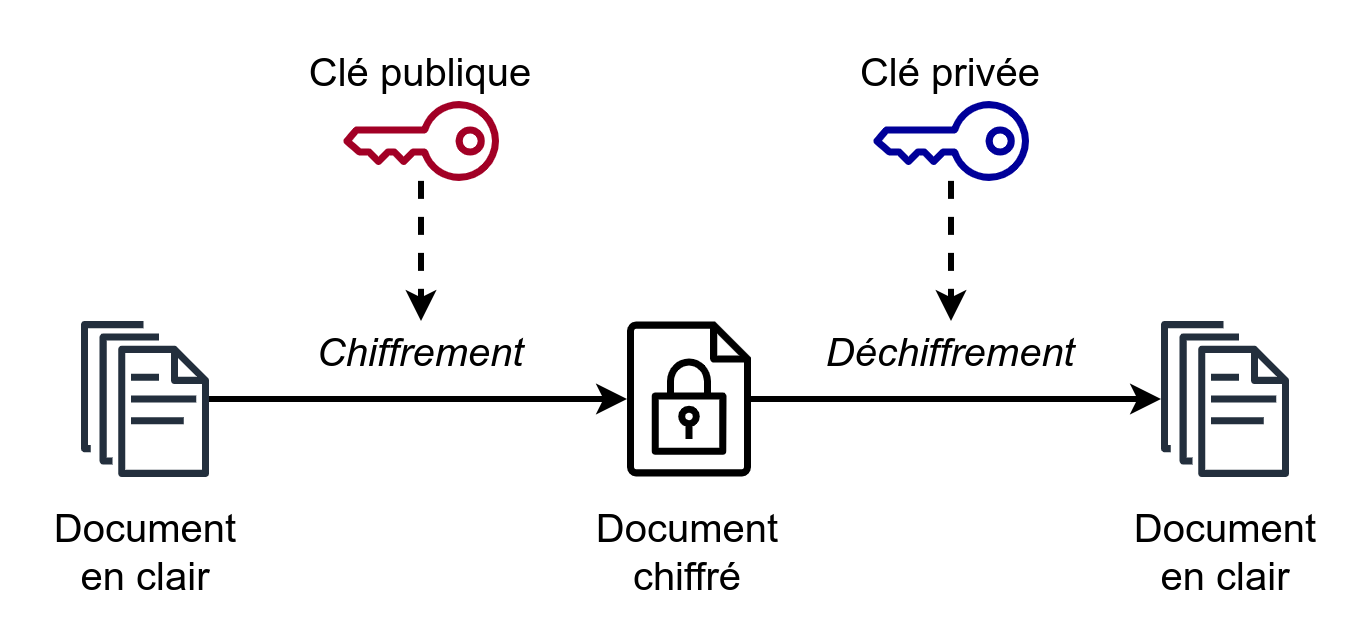
Présentation
On pourrait modéliser le procédé avec des cadenas et des clés. D'abord, Alice diffuse au mode entier un nombre illimité de cadenas identiques qui peuvent être ouverts uniquement par la clé qu'elle garde bien secrètement pour elle. Si Bob veut envoyer un message à Alice et être sûr que seule Alice peut le lire, il a juste à se procurer un coffre, à y déposer le message pour Alice et à le fermer avec le fameux cadenas. Ensuite, Bob envoie le coffre à Alice, qu'elle pourra ouvrir avec sa clé.Dans l'algorithme RSA, premier algorithme de cryptographie asymétrique, chaque individu possède deux clés : une clé publique et une clé privée. Dans l'analogie précédente, la clé publique correspond aux cadenas et la clé privée correspond à la clé du cadenas. Comme leur nom l'indique, la clé publique est accessible par tous, et la clé privée doit absolument rester secrète. Les clés vont de pair : la clé publique sert à chiffrer un message et la clé privée permet de déchiffrer un message codée avec la clé publique associée.
Par exemple, imaginons que Alice veuille envoyer un message à Bob. Pour ce faire, il récupère la clé publique d'Alice, et encode le message avec. Ensuite, Alice, seule détentrice de la clé privée, peut déchiffrer le message codé que lui a envoyé Bob.
Histoire
Le concept de cryptographie asymétrique est attribué à Whitfield Diffie et Martin Hellman en 1976. Le premier algorithme fonctionnel est l'algorithme RSA, des initiales des trois chercheurs l'ayant mis au point en 1977 : Ronald Rivest, Adi Shamir et Leonard Adleman.Une condition indispensable est qu'il soit « calculatoirement impossible » de déchiffrer à l'aide de la seule clé publique, en particulier de reconstituer la clé privée à partir de la clé publique, c'est-à-dire que les moyens de calcul disponibles et les méthodes connues au moment de l'échange (et le temps que le secret doit être conservé) ne le permettent pas.
Histoire
Voici le principe mathématique derrière l'algorithme RSA à travers un exemple.- On va choisir deux nombres premiers (pas trop grands ici pour la simplicité de l'exemple, mais dans la pratique il faut choisir des nombres très grand), ici p = 3 et q = 11.
- On calcule n = pq = 3 * 11 = 33.
- On calcule phi(n) = (p - 1)(q - 1) = 2 * 10 = 20.
- Choisir e tel que 1 < e < phi(n) et e et phi(n) sont premiers entre eux. On prend e = 7.
- Choisir un d tel que de % phi(n) = 1 : le reste de la division euclidienne de de = 7d par phi(n) = 20 est 1. On prend d = 3.
- On définit la clé publique : (e, n) = (7, 33).
- On définit la clé privée : (d, n) = (3, 33).
- Si on veut encoder m = 2, on calcule c = 2^e % n = 2^7 % 33 = 29.
- Si on veut décoder c = 29, on calcule m = 2^d % n = 29^3 % 33 = 2.