Jeu web d'introduction à la cryptographie
J'ai perdu
Comment ça marche ?

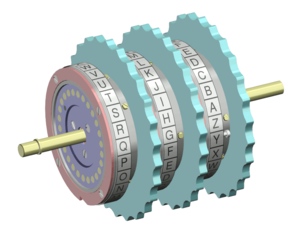
L'unité d'encryptage est composée de 3 gros rotors en caoutchouc parcourus de fils, d'un réflecteur et d'un tableau de connexion où l'opérateur pouvait relier deux lettres par des câbles.
Fonctionnement d'un seul rotor

Le rotor permet de faire passer le courant venant des lettres sur le clavier aux lettres sur le tableau d'affichage. Chaque fil relie deux lettres.
Chaque fois que l'utilisateur entrera une lettre, le courant allant de la lettre selectionnée jusqu'à la sortie du rotor indiquera en quelle lettre la lettre entrée par l'utilisateur sera encryptée. Cependant, après l'encryptage de chaque lettre, le rotor effectue une rotation de 1/26 afin que l'encryptage ne soit pas toujours le même.
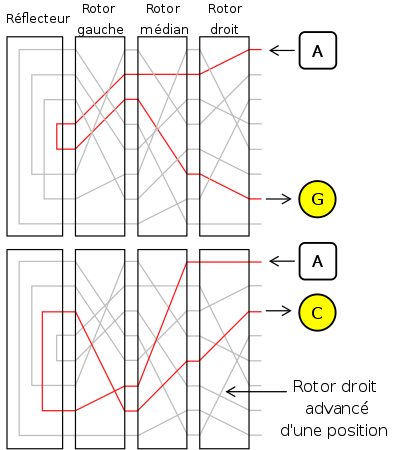
Fonctionnement de la machine Enigma sans réflecteur ni tableau de connection

Le fonctionnement du réflecteur
Le tableau de connection
Pour augmenter l'encryptage, chaque opérateur avait la possibilité d'utiliser un ou plusieurs câbles pour connecter des lettres entre elles. Ainsi, si par exemple l'opérateur décidait de connecter les lettres A et B, lorsque la lettre A serait appuyée, elle serait encryptée comme le serait la lettre B et inversement. Un aléa pouvait donc être rajouté sans changer les rotors.La machine Enigma dans l'armée allemande
Dans l'armée allemande, la machine Enigma était composée de plus de rotors. À partir de 1939, les machines avaient au moins 5 rotors, sans changer le reste du fonctionnement de la machine. Chacun était numéroté, et seuls 3 étaient choisis pour être dans les machines. Dans la marine allemande, le nombre de rotors monta jusqu'à 8, et son fonctionnement était légèrement différent.Les clés
Pour pouvoir échanger des messages avec une autre personne ayant aussi une machine Enigma, il faut que cette autre personne ait la même clé que vous, c'est-à-dire que les positions initiales de vos rotors, leur ordre et les lettres connectées par des câbles soient les mêmes! Ainsi, pour que vos conversations ne soient pas décryptées, il faut que votre clé partagée reste secrète...Nombre d'arrangements de lettres possibles
Sans utiliser les câbles ni changer l'ordre des rotors :Avec 3 rotors, il y a 263 soit 17 756 arrangements possibles.
Avec 5 rotors, il y a 265 arrangements possibles soit : 11 881 376 arrangements.
Si nous considérerions changer l'ordre des rotors, et que nous avions n rotors, il faudrait ajouter un facteur n! aux valeurs calculées précédemment.
Si nous souhaitions de plus utiliser les câbles, en supposant que nous en avons m, il faudrait rajouter un facteur : $$ 26! \over m!(26-2m)!2^m $$ Pour 6 câbles, ce facteur vaut 100 391 791 500
Histoire
En 1918, Arthur Scherbius et Richard Ritter fondèrent Scherbius&Ritter, une entreprise d'ingénieurie innovante qui traitait de nombreux problèmes allant des oreillers chauffants aux turbines. Scherbius était en charge de la recherche et développement au sein de l'entreprise et souhaitait créer un nouveau système de cryptographie qui succéderait à ceux de la première guerre mondiale qui était inadéquat. La machine Enigma fut inventée par Scherbius et fût utilisée principalement par l'Allemagne Nazie, à partir de 1926, mais aussi par d'autres nations pour protéger leurs messages diplomatiques et militaires.Durant la seconde guerre mondiale, les soldats allemands possédaient des carnets contenant les clés d'encryptage pour chaque jour. Cependant, pour limiter le risque d'usure de clé, lorsqu'ils souhaitaient communiquer, ils envoyaient également une clé deux fois (si la nouvelle clé est PGN, le message contenant la clé serait PGNPGN) grâce à la clé du jour qui indiquait une nouvelle disposition des rotors, rendant la tâche de décryptage plus ardue.
Craquer le code
En 1931, le service français de renseignement obtint d'une source les premières copies de documentation sur la machine, et une collaboration s'instaura avec les services d'intelligence britannique pour craquer cette méthode de cryptographie qui dura jusqu'en 1939. La machine fut aussi reproduite par des services polonais, grâce à de la documentation sur la machine de plus en plus précise, qui a l'époque, ne contenait que 3 rotors.Rejewski
En 1932, 3 mathématiciens polonais parvinrent à décrypter des messages de l'Enigma. En 1938, l'un deux, Rejewski, réussi à créer un déchiffrage par une machine électronique qui prenait 2h pour trouver la clé du jour.Pour décrypter des messages, Rejewski s'intéressa aux répétitions, en effet, les répétitions sont les ennemies de la sécurité!

Ainsi, une fois qu'il avait les positions des rotors, il lui suffisait d'essayer de décrypter des messages avec les différents ordres de rotors possibles (6 à l'époque) et de voir quelles lettres auraient pû être échangées. Par exemple, si le message donnait "purtde rutterdam", le u et le o étaient échangés, donc connectés par un câble!
Les machines contenant les différents arrangements des rotors étaient appellées "bombes électromagnétiques". En décembre 1938, les allemands augmentèrent la sécurité de leur machine Enigma en lui ajoutant 2 rotors, et Rejewski ne put en venir à bout. Il lui aurait fallu 60 "bombes", et elles coutaient très chères, en avoir 60 nécessiterait 6 fois le budget annuel du Biuro, l'endroit où il travaillait. Puis, l'armée allemande augmenta également le nombre de câbles pour échanger des lettre, il passa de 6 à 10. Le nombre de clés possibles étaient à présent de 159 x 10 18.
En juillet 1939, ils transmirent aux services français et britanniques qui jusque là, pensait que le code d'Enigma était incassable, un exemplaire d'Enigma ainsi que la documentation sur le décryptage. Ils virent également l'importance d'utiliser les mathématiciens pour casser des codes. Jusque là, leurs équipes étaient en grande majorité composées de linguistes.
Bletchey Park, Buckinghamshire
Bletchey Park fut l'endroit où les nouvelles recrues se concentrèrent sur le problème de décryption d'Enigma. En 5 ans, l'endroit finit par comprendre 7000 personnes.Chaque jours, ils cherchaient à déterminer la clé du jour en se basant sur la méthode de Rejewski, ce qui pouvait prendre plusieurs heures, et finissaient par déchiffrer les messages accumulés.
Les services anglais découvrir quelques facteurs qui aidèrent à raccourcir le temps pour déterminer la clé. Par exemple, bien que les allemands étaient censés prendre des lettres aléatoires pour leur clé de communication, ils avaient tendance à choisir des lettres consécutives. De plus, chaque rotor ne restait pas plus d'une journée à la même position, cela divisait par deux le nombre de clés possibles. Par exemple, si le premier jour on avait comme disposition des rotors 123, on ne pouvait pas avoir le jour suivant 213. Il était aussi impossible d'échanger deux lettres à la suite l'une de l'autre sur le clavier.
En 1939, Alan Turing fut recruté pour travailler à Bletchey Park. Turing s'est concentré sur le fait qu'il était possible que les allemand ne demandent plus à leurs troupes de répéter deux fois la clé, si ils se rendaient compte que cela permettaient de craquer leur code, et qu'ils ne tarderaient pas à le remarquer. Il s'est alors interessé à la grande quantité de messages déjà décryptés, et s'est rendu compte que leur construction était assez rigide. Par exemple, tous les jour, à environ 6h, un rapport météo était envoyé, et donc contenait presque toujours le mot "wetter", soit en français "météo".

Bien qu'à présent la décryption fut automatisée, ils ne pouvaient toujours pas casser le code d'Enigma pour la marine allemande. Des vols de clés furent planifiés pour obtenir ces informations.
Les informations obtenues en déchiffrant les messages d'Enigma furent précieuses pour le camp des Alliés, il fut estimé que la décryption de ces messages permit d'écourter la guerre de 2 ans. Cependant, certaines décisions de l'armée britannique ont fait débat. Des informations furent décryptées sur des attaques, et les Alliés décidèrent parfois de ne pas agir, afin de ne pas rendre les allemands suspicieux et les amener à changer leur méthode de cryptage ou suspecter que leurs clés avaient fuitées.
Sources
Wikipédia : Enigma(machine)The Code Book, Simon Singh (pages 146 à 211)
Nombre de câblages possibles